type
status
date
slug
summary
tags
category
icon
password
不相交的线
在两条独立的水平线上按给定的顺序写下
nums1 和 nums2 中的整数。现在,可以绘制一些连接两个数字
nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:nums1[i] == nums2[j]
- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:
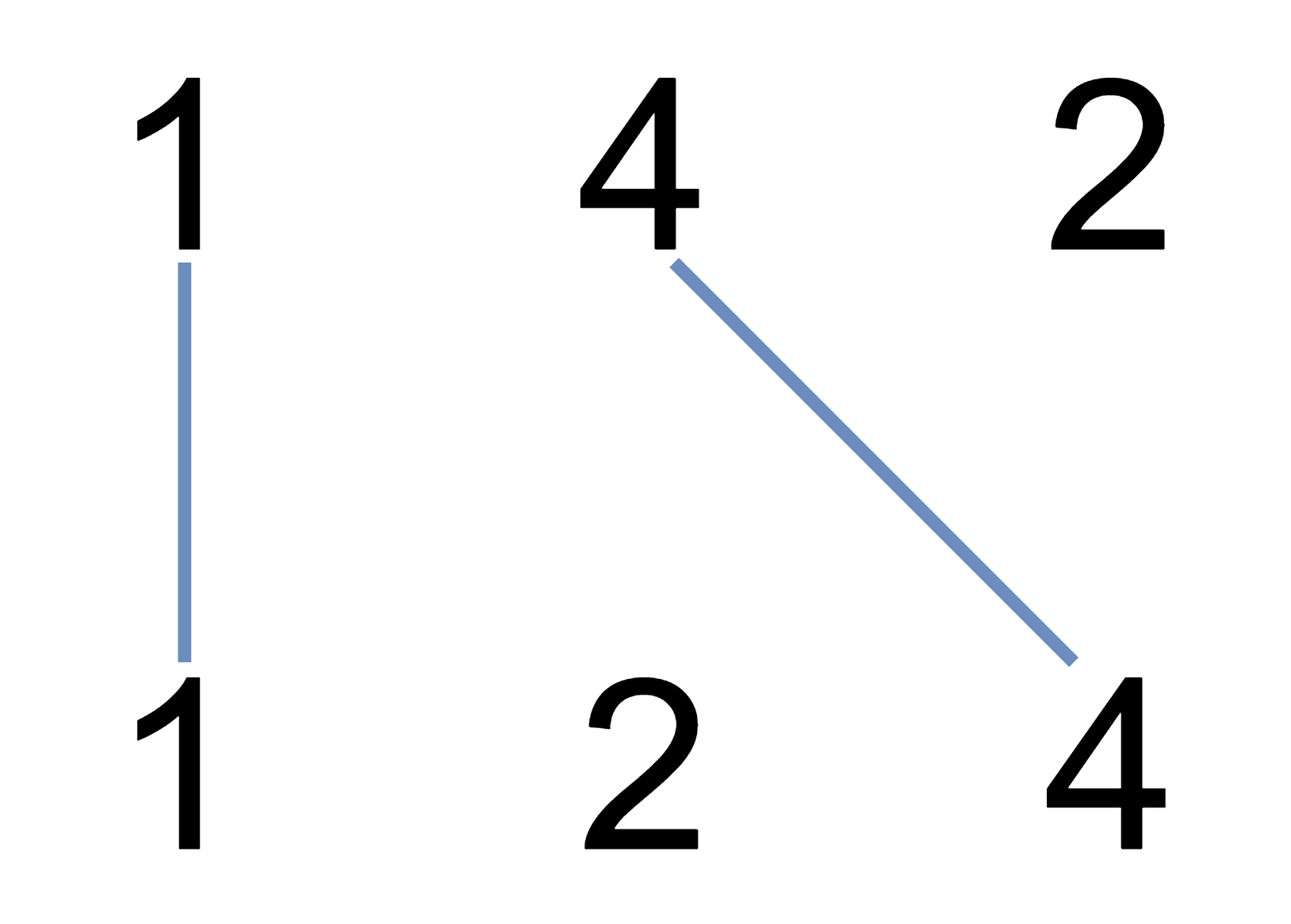
示例 2:
示例 3:
提示:
1 <= nums1.length, nums2.length <= 500
1 <= nums1[i], nums2[j] <= 2000
题解
分析
动态规划
给定两个数组
nums1 和 nums2 ,当 nums1[i] == nums2[j] 时,可以用一条直线连接 nums1[i] 和 nums2[j] 。假设一共绘制了 k 条不相交的直线,其中 x 条直线连接 num1[ix] 和 nums2[jx] ,则对于任意 1 ≤ x ≤ k 都有 nums1[ix] == num2[jx] ,其中 i1 < i2 < …ik, j1 < j2 < …jk 。上述
k 条互不相交的直线分别连接了数组 nums1 和 nums2 的 k 对相等的元素,而且这 k 对相等的元素在两个数组中的相对顺序是一致的,因此,这 k 对相等的元素组成的序列即为数组 nums1 和 nums2的公共子序列。要计算可以绘制的最大连线数,即为计算数组 nums1和 nums2的最长公共子序列的长度。最长公共子序列问题是典型的二维动态规划问题。假设数组 nums1和nums2的长度分别为 m 和 n,创建 m+1 行 n+1 列的二维数组 dp,其中 dp[i][j] 表示 nums1[0:i] 和 nums2[0:j] 的最长公共子序列的长度。上述表示中,nums1[0:i]表示数组nums1的长度为i的前缀,nums2[0:j]表示数组nums2的长度为j的前缀。

代码
附录
- Author:Zinphy
- URL:https://zouysay.cn/article/dfcf3ada-8f95-400b-9736-15133a81de20
- Copyright:All articles in this blog, except for special statements, adopt BY-NC-SA agreement. Please indicate the source!